How Many Different Hands Are Possible In Texas Holdem
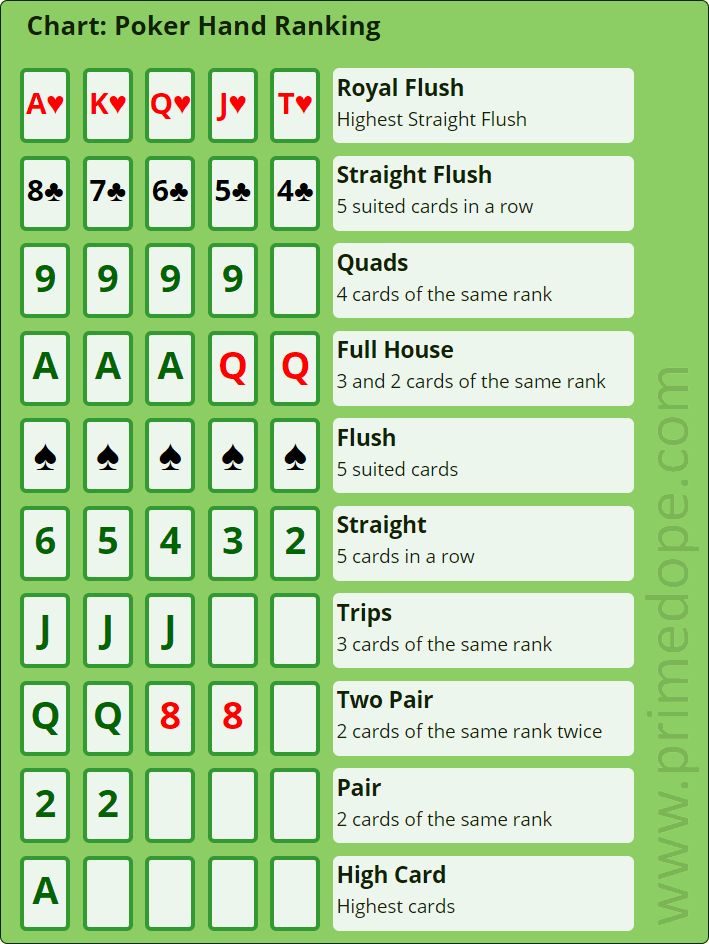
Don't worry if you don't know why we do this, just take it as it is. This means that the probability of the flop being A K Q in any order is 1/19,600 - which is exactly the same probability as the flop coming something like 2 5 9 in any order. So in total there are 19,600 different possible flops. Next in the poker hands list is a straight, consisting of a run of five cards of consecutive values, such as 4-5-6-7-8. Aces count as high or low, so you can make a 10-J-Q-K-A straight, the highest, or an A-2-3-4-5 straight, which is the lowest and sometimes called a “wheel”.
In the poker game of Texas hold 'em, a starting hand consists of two hole cards, which belong solely to the player and remain hidden from the other players. Five community cards are also dealt into play. Betting begins before any of the community cards are exposed, and continues throughout the hand. The player's 'playing hand', which will be compared against that of each competing player, is the best 5-card poker hand available from his two hole cards and the five community cards. Unless otherwise specified, here the term hand applies to the player's two hole cards, or starting hand.
- Ever since the early days of Texas holdem poker, players have attempted to analyze and organize the 169 possible two card starting hands found in the game. One traditional way of doing so involves running thousands upon thousands of simulations in which a particular holdem hand is played out against nine random opponent hands.
- How Many Possible Texas Holdem Hands Are There Every This means there are 3 times as many offsuit (non-pair) hands compared to suited. In total there are 154 hand types which are not pocket-pairs. 78 of these are suited, 78 of these are offsuit.
Essentials[edit]
There are 1326 distinct possible combinations of two hole cards from a standard 52-card deck in hold 'em, but since suits have no relative value in this poker variant, many of these hands are identical in value before the flop. For example, A♥J♥ and A♠J♠ are identical in value, because each is a hand consisting of an ace and a jack of the same suit.
Therefore, there are 169 non-equivalent starting hands in hold 'em, which is the sum total of : 13 pocket pairs, 13 × 12 / 2 = 78 suited hands and 78 unsuited hands (13 + 78 + 78 = 169).
These 169 hands are not equally likely. Hold 'em hands are sometimes classified as having one of three 'shapes':
- Pairs, (or 'pocket pairs'), which consist of two cards of the same rank (e.g. 9♠9♣). One hand in 17 will be a pair, each occurring with individual probability 1/221 (P(pair) = 3/51 = 1/17).
- Alternative means of making this calculation
- First Step
- As confirmed above.
- There are 1326 possible combination of opening hand.
- Second Step
- There are 6 different combos of each pair. 9h9c, 9h9s, 9h9d, 9c9s, 9c9d, 9d9s. Therefore, there are 78 possible combinations of pocket pairs (6 multiplied by 13 i.e. 22-AA)
- To calculate the odds of being dealt a pair
- 78 (the number of any particular pair being dealt. As above) divided by 1326 (possible opening hands)
- 78/1326 = 0.058 or 5.8%
- Suited hands, which contain two cards of the same suit (e.g. A♣6♣). 23.5% of all starting hands are suited.
Probability of first card is 1.0 (any of the 52 cards)Probability of second hand suit matching the first:There are 13 cards per suit, and one is in your hand leaving 12 remaining of the 51 cards remaining in the deck. 12/51=.2353 or 23.5%
- Offsuit hands, which contain two cards of a different suit and rank (e.g. K♠J♥). 70.6% of all hands are offsuit hands
Offsuit pairs = 78Other offsuit hands = 936
It is typical to abbreviate suited hands in hold 'em by affixing an 's' to the hand, as well as to abbreviate non-suited hands with an 'o' (for offsuit). That is,
- QQ represents any pair of queens,
- KQ represents any king and queen,
- AKo represents any ace and king of different suits, and
- JTs represents any jack and ten of the same suit.
Limit hand rankings[edit]
Some notable theorists and players have created systems to rank the value of starting hands in limit Texas hold'em. These rankings do not apply to no limit play.
Sklansky hand groups[edit]
David Sklansky and Mason Malmuth[1] assigned in 1999 each hand to a group, and proposed all hands in the group could normally be played similarly. Stronger starting hands are identified by a lower number. Hands without a number are the weakest starting hands. As a general rule, books on Texas hold'em present hand strengths starting with the assumption of a nine or ten person table. The table below illustrates the concept:
Chen formula[edit]
The 'Chen Formula' is a way to compute the 'power ratings' of starting hands that was originally developed by Bill Chen.[2]
- Highest Card
- Based on the highest card, assign points as follows:
- Ace = 10 points, K = 8 points, Q = 7 points, J = 6 points.
- 10 through 2, half of face value (10 = 5 points, 9 = 4.5 points, etc.)
- Pairs
- For pairs, multiply the points by 2 (AA=20, KK=16, etc.), with a minimum of 5 points for any pair. 55 is given an extra point (i.e., 6).
- Suited
- Add 2 points for suited cards.
- Closeness
- Subtract 1 point for 1 gappers (AQ, J9)
- 2 points for 2 gappers (J8, AJ).
- 4 points for 3 gappers (J7, 73).
- 5 points for larger gappers, including A2 A3 A4
- Add an extra point if connected or 1-gap and your highest card is lower than Q (since you then can make all higher straights)
Phil Hellmuth's: 'Play Poker Like the Pros'[edit]
Phil Hellmuth's 'Play Poker Like the Pros' book published in 2003.
| Tier | Hands | Category |
|---|---|---|
| 1 | AA, KK, AKs, QQ, AK | Top 12 Hands |
| 2 | JJ, TT, 99 | |
| 3 | 88, 77, AQs, AQ | |
| 4 | 66, 55, 44, 33, 22, AJs, ATs, A9s, A8s | Majority Play Hands |
| 5 | A7s, A6s, A5s, A4s, A3s, A2s, KQs, KQ | |
| 6 | QJs, JTs, T9s, 98s, 87s, 76s, 65s | Suited Connectors |
Statistics based on real online play[edit]
Statistics based on real play with their associated actual value in real bets.[3]
| Tier | Hands | Expected Value |
|---|---|---|
| 1 | AA, KK, QQ, JJ, AKs | 2.32 - 0.78 |
| 2 | AQs, TT, AK, AJs, KQs, 99 | 0.59 - 0.38 |
| 3 | ATs, AQ, KJs, 88, KTs, QJs | 0.32 - 0.20 |
| 4 | A9s, AJ, QTs, KQ, 77, JTs | 0.19 - 0.15 |
| 5 | A8s, K9s, AT, A5s, A7s | 0.10 - 0.08 |
| 6 | KJ, 66, T9s, A4s, Q9s | 0.08 - 0.05 |
| 7 | J9s, QJ, A6s, 55, A3s, K8s, KT | 0.04 - 0.01 |
| 8 | 98s, T8s, K7s, A2s | 0.00 |
| 9 | 87s, QT, Q8s, 44, A9, J8s, 76s, JT | (-) 0.02 - 0.03 |
Nicknames for starting hands[edit]
In poker communities, it is common for hole cards to be given nicknames. While most combinations have a nickname, stronger handed nicknames are generally more recognized, the most notable probably being the 'Big Slick' - Ace and King of the same suit, although an Ace-King of any suit combination is less occasionally referred to as an Anna Kournikova, derived from the initials AK and because it 'looks really good but rarely wins.'[4][5] Hands can be named according to their shapes (e.g., paired aces look like 'rockets', paired jacks look like 'fish hooks'); a historic event (e.g., A's and 8's - dead man's hand, representing the hand held by Wild Bill Hickok when he was fatally shot in the back by Jack McCall in 1876); many other reasons like animal names, alliteration and rhyming are also used in nicknames.
Notes[edit]
- ^David Sklansky and Mason Malmuth (1999). Hold 'em Poker for Advanced Players. Two Plus Two Publications. ISBN1-880685-22-1
- ^Hold'em Excellence: From Beginner to Winner by Lou Krieger, Chapter 5, pages 39 - 43, Second Edition
- ^http://www.pokerroom.com/poker/poker-school/ev-stats/total-stats-by-card/[dead link]
- ^Aspden, Peter (2007-05-19). 'FT Weekend Magazine - Non-fiction: Stakes and chips Las Vegas and the internet have helped poker become the biggest game in town'. Financial Times. Retrieved 2010-01-10.
- ^Martain, Tim (2007-07-15). 'A little luck helps out'. Sunday Tasmanian. Retrieved 2010-01-10.
This means there are 3 times as many offsuit (non-pair) hands compared to suited. In total there are 154 hand types which are not pocket-pairs. 78 of these are suited, 78 of these are offsuit. Since there are 4 combos of every suited hand this results in (78. 4) 312 combos. In Texas Hold’em, there are three roles that rotate clockwise after each game: Dealer, Left Blind, and Right Blind. Poker hands odds & outs: a crash course-guide on poker odds, pot odds, probabilities & odds charts so you can win at Texas Hold’em at the tables or online. One of the most important things that a poker player should know is what their poker odds are in a given situation.
For a certain segment of new hold’em players, starting hand charts can be fascinating. Even those with many years of experience who have little need to consult such charts still find them interesting as debate-starters.
In hold’em there are 169 different combinations of hands you can be dealt. For those of us who enjoy working with numbers or creating lists with which to organize our lives, there’s something appealing about the idea of ranking all of those hands from 1 to 169, even if we know such a list probably might have only limited value when it comes to actual game play.
In truth, there are actually a lot more possible combinations of hole cards in hold’em — 1,326 of them, in fact. But that total also considers suits as distinct, when in fact before the community cards come the suits are all essentially of equal value.
That is to say, is of the same value as when playing preflop, while and are also of equivalent value. So, too, are the different combinations producing the same pocket pairs all equal before the flop in terms of their relative worth. While there are six different ways to get pocket aces — , , , , , — you're equally happy no matter what suits the cards are.
So we get rid of all of those redundant hands and say that in Texas hold'em there are 169 “non-equivalent” starting hands, breaking them down as follows:
- 13 pocket pairs
- 78 non-paired suited hands (e.g., with two cards of the same suit like or )
- 78 non-paired unsuited hands (e.g., with two cards of different suits like or )
Notice now the non-paired combinations of hole cards neatly divide into equal groups, both of which are six times as large (78) as the smaller group of pocket pairs (13). The total of 169 combinations represents a square, too — 13 x 13 — another curious symmetry when it comes to hold'em hands.
Still, that’s a lot of starting hand combinations — too many for most of us humans to keep in our heads — which is one reason hand ranking charts are appealing and even can be useful, since they help players think about certain two-card combos as “strong” or “average” or “weak” as possible starters.
Setting aside the idea of actually ranking the 169 hands from best to worst, we might think for a moment about other ways of categorizing starting hands in hold’em, using that initial breakdown of hands into pocket pairs, non-paired suited hands, and non-paired unsuited hand as a first step toward coming up with further, smaller groups that are easier to remember.
How Many Possible Texas Holdem Hands Are There Time
The 13 pocket pairs we might group as big or “premium” (, , and ), medium ( through ), and small ( through ).

Meanwhile, we might divide each of the other groups into “connectors,” “one-gappers,” and “two-gappers” (and so on), further thinking of them also as “big,” “medium,” and “small” while also keeping separate suited and non-suited combinations.
These categories of non-paired hands are created by thinking about straight-making possibilities (affected by connectedness) and flush-making possibilties (affected by suitedness). There are more ways to make straights with “connectors” — that is, two cards of consecutive rank like — than with two-gappers, three-gappers, and so on. So, too, do you have a better chance of making a flush with suited hole cards than with non-suited hole cards.
Another possible group to create would include “ace hands” — i.e., non-paired hands containing one ace — that can be thought of as “big aces” (e.g., , ), “medium aces” ( down to ), and “small aces” ( to ). Or “king hands,” too. We like keeping these groups in mind, as hands with big cards like an ace or king can connect with flops to make big pairs.
In any case, you can see how these criteria for making categories can help when it comes to building those starting hand charts. And in fact most of those charts feature a similar ordering of hands, with..
- the premium pocket pairs and the big aces (suited and non-suited) up at the top;
- medium and small pocket pairs and big-to-medium suited connectors and one-gappers in the middle;
- and non-paired hands with less potential to make big pairs, straights, or flushes toward the bottom.
Would you like to get your hands on a free $10k entry to the WSOP Main Event?
Click on the link below and enter your email to participate to the free giveaway and take a shot at this massive opportunity!
Play NowHowever, there are problems with relying so heavily on starting hand charts that you don’t take into account factors that can make a given hand gain or lose value. Such as the flop. Or the turn. Or the river. Or other factors — including how your opponents are playing their hands — that can quickly affect the value of your starting hands.
After all, as anyone who’s played even a few hands of hold’em well knows, even if is the highest-ranking starting hand and a non-suited ranks as 169th, a couple of deuces among the community cards is all it takes to make the best hand worst and the worst hand best.
Learning the relative value of starting hands is definitely an important first step when it comes to getting started in hold’em. Other aspects of game play such as the importance of position, knowing when and how much to bet or raise, and thinking about opponents’ holdings and playing styles as hands proceed are good to learn, too, and help show how a great starting hand might not be so great five community cards later.
Poker is not blackjack, a game in which similar hand-ranking guides are sometimes used to inform players’ decisions about how to play. In poker you want to be wary about becoming too reliant on those pretty starting hand charts. They can be great for indicating which hands might be worth playing (and which should be thrown away), but troublesome if allowed to outweigh all of the other important factors that arise as a hand plays out.
That said, starting hand charts can be useful, especially for those new to hold’em. They also can be a big help when picking up other games, too, like pot-limit Omaha or the various stud games, if only to get an early idea what hands tend to play better than others.
But for many such charts ultimately are only themselves a way to get started, before the experience of playing helps players more instinctively recognize both hand groupings and how hands tend to compare in terms of profitability.
Get all the latest PokerNews updates on your social media outlets. Follow us on Twitter and find us on both Facebook and Google+!
Tags
no-limit hold’emcash game strategytournament strategybeginner strategystarting hand selectionstarting hand chartsmath
Poker can be a fun card game for the family, or a serious competitive game in which the steaks can be so enormous, even selling your house wouldn’t cover the costs.
There are many variations of poker, with Texas Hold ‘Em being the most popular worldwide.
Below are a whole bunch of poker facts and statistics which help you understand the chances of wining and the odds of getting the cards you want.
Did You Know?
A pocket pair is cards of the same rank, which means if your two cards have the same number, from 2-2 all the way up to A-A, this is called a pocket pair.
- The odds of receiving any pocket pair is 5.9% which is 16 to 1. These are also the same odds of receiving a pocket pair of 2’s.
- The odds of receiving a specific pocket pair: 0.45% or 220 to 1 These are the same odds for receiving a pocket pair of A’s.
- The odds of receiving a pocket pair of A’s twice in a row is 0.002047% or 48,840 to 1.
- The odds of receiving a pocket pair of K’s is 0.9% which is 220 to 1.
- The odds of receiving a pocket pair of Q’s is 1.4% which is 73 to 1.
- The odds of receiving a pocket pair of J’s is 1.8% which is 54 to 1.
- The odds of receiving a pocket pair of 10’s is 2.3% which is 43 to 1.
- The odds of receiving a pocket pair of 9’s is 2.7% which is 36 to 1.
- The odds of receiving a pocket pair of 8’s is 3.2 which is 31 to 1.
- The odds of receiving a pocket pair of 7’s is 3.6% which is 27 to 1.
- The odds of receiving a pocket pair of 6’s is 4.1% which is 24 to 1.
- The odds of receiving a pocket pair of 5’s is 4.5% which is 21 to 1.
- The odds of receiving a pocket pair of 4’s is 5.0% which is 19 to 1.
- The odds of receiving a pocket pair of 3’s is 5.4% which is 17 to 1.
Poker Fast Facts
The total number of possible royal flush hands in a standard 52 card deck is 4.
And the odds of making a royal flush is 649,739 to 1.
This is correct assuming that every game plays to the river.
In poker terms, the river is the name for the fifth card dealt, face-up on the board.
How Many Different Hands Are Possible In Texas Holdem Tournaments
In total, there are 2,598,960 possible poker hands with 52 cards.
The odds of getting four of a kind in Texas Hold ‘Em is 4164 to 1.
Casinos normally change decks after 15 minutes of steady play, so that the cards can always be fresh and unmarked, as many professional players would be able to remember the certain markings on cards and use that to their advantage.
This is only a basic overview of poker odds, there are many calculators online that can help solve the odds of getting certain hands, depending on what stage of the game you’re at, what cards you currently hold and how many people are playing.
Now you are familiar with these odds, you can use them to your advantage for a better poker strategy when you finally decided to play a tournament. Casino online, free bonus no deposit usa.
How Many Possible Texas Holdem Hands Are There Every
How Many Different Hands In Texas Holdem
In Texas Hold-Em Poker the odds of making a royal flush hand is only 649,739 to 1.